Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 156, pp. 1-39.
Nodal solutions for singular second-order boundary-value problems
Abdelhamid Benmezai, Wassila Esserhane, Johnny Henderson
Abstract:
We use a global bifurcation theorem to prove the existence of
nodal solutions to the singular second-order two-point boundary-value
problem
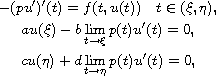
where
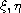 ,
,
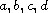 are real numbers with
are real numbers with
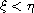 ,
,
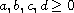 ,
,
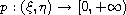 is a measurable
function with
is a measurable
function with
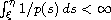 and
and
![$f:[ \xi ,\eta ] \times [ 0,+\infty) \to [ 0,+\infty ) $](gifs/ah.gif) is a Caratheodory function.
is a Caratheodory function.
Submitted January 27, 2014. Published July 7, 2014.
Math Subject Classifications: 34B15, 34B16, 34B18.
Key Words: Singular second-order BVPs; nodal solutions;
global bifurcation theorem.
Show me the PDF file (463 KB),
TEX file for this article.
 |
Abdelhamid Benmezai
Faculty of Mathematics, USTHB, Algiers, Algeria
email: aehbenmezai@gmail.com
|
|---|
 |
Wassila Esserhane
Graduate School of Statistics and Applied Economics
P.O. Box 11, Doudou Mokhtar
Ben-Aknoun Algiers, Algeria
email: ewassila@gmail.com
|
|---|
 |
Johnny Henderson
Department of Mathematics, Baylor University
Waco, Texas 76798-7328, USA
email: Johnny_Henderson@baylor.edu
|
|---|
Return to the EJDE web page
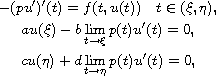
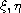 ,
,
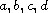 are real numbers with
are real numbers with
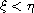 ,
,
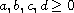 ,
,
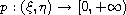 is a measurable
function with
is a measurable
function with
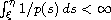 and
and
![$f:[ \xi ,\eta ] \times [ 0,+\infty) \to [ 0,+\infty ) $](gifs/ah.gif) is a Caratheodory function.
is a Caratheodory function.


