Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 160, pp. 1-13.
Stability of parabolic equations with unbounded operators
acting on delay terms
Allaberen Ashyralyev, Deniz Agirseven
Abstract:
In this article, we study the stability of the initial value problem for the
delay differential equation

in a Banach space E with the unbounded linear operators A and
B(t) with dense domains
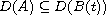 .
We establish stability estimates for the solution of this problem in
fractional spaces
.
We establish stability estimates for the solution of this problem in
fractional spaces
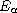 .
Also we obtain stability
estimates in Holder norms for the solutions of the mixed problems
for delay parabolic equations with Neumann condition with respect to space
variables.
.
Also we obtain stability
estimates in Holder norms for the solutions of the mixed problems
for delay parabolic equations with Neumann condition with respect to space
variables.
Submitted April 14, 2014. Published July 21, 2014.
Math Subject Classifications: 35K30.
Key Words: Delay parabolic equation; stability estimate;
fractional space; Holder norm.
Show me the PDF file (240 KB),
TEX file for this article.
 |
Allaberen Ashyralyev
Department of Mathematics, Fatih University
34500 Buyukcekmece
Istanbul, Turkey
email: aashyr@fatih.edu.tr
|
|---|
 |
Deniz Agirseven
Department of Mathematics, Trakya University
22030, Edirne, Turkey
email: denizagirseven@yahoo.com
|
|---|
Return to the EJDE web page

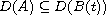 .
We establish stability estimates for the solution of this problem in
fractional spaces
.
We establish stability estimates for the solution of this problem in
fractional spaces
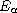 .
Also we obtain stability
estimates in Holder norms for the solutions of the mixed problems
for delay parabolic equations with Neumann condition with respect to space
variables.
.
Also we obtain stability
estimates in Holder norms for the solutions of the mixed problems
for delay parabolic equations with Neumann condition with respect to space
variables.

