Fatori and Rivera [7] studied the stability of the Bresse system with one distributed temperature dissipation law operating on the angle displacement equation. They proved that, in general, the energy of the system does not decay exponentially and they established the rate of
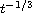 .
In this article, our goal is to extend their results, by taking into
consideration the important case when the thermal dissipation is locally
distributed and to improve the polynomial energy decay rate.
We then study the energy decay rate of Bresse system with one locally
thermal dissipation law. Under the equal speed wave propagation condition,
we establish an exponential energy decay rate. On the contrary,
we prove that the energy of the system decays, in general,
at the rate
.
In this article, our goal is to extend their results, by taking into
consideration the important case when the thermal dissipation is locally
distributed and to improve the polynomial energy decay rate.
We then study the energy decay rate of Bresse system with one locally
thermal dissipation law. Under the equal speed wave propagation condition,
we establish an exponential energy decay rate. On the contrary,
we prove that the energy of the system decays, in general,
at the rate
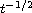 .
.

