Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 186, pp. 1-12.
Asymptotic behavior of solutions to higher order nonlinear delay
differential equations
Haihua Liang
Abstract:
In this article, we study the oscillation and asymptotic behavior of solutions
to the nonlinear delay differential equation
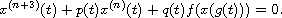
By using a generalized Riccati transformation and an integral averaging technique,
we establish sufficient conditions for all solutions to oscillate, or to
converge to zero. Especially when the delay has the form
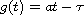 ,
we provide two convenient oscillatory criteria.
Some examples are given to illustrate our results.
,
we provide two convenient oscillatory criteria.
Some examples are given to illustrate our results.
Submitted June 27, 2014. Published September 3, 2014.
Math Subject Classifications: 34K11, 34K25.
Key Words: Higher order differential equation; delay differential equation,
asymptotic behavior; oscillation.
Show me the PDF file (234 KB),
TEX file for this article.
 |
Haihua Liang
Department of Computer Science
Guangdong Polytechnic Normal University
Guangzhou, Guangdong 510665, China
email: haiihuaa@tom.com
|
|---|
Return to the EJDE web page
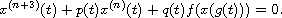
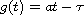 ,
we provide two convenient oscillatory criteria.
Some examples are given to illustrate our results.
,
we provide two convenient oscillatory criteria.
Some examples are given to illustrate our results.
