Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 227, pp. 1-13.
A compactness lemma of Aubin type and its application to degenerate
parabolic equations
Anvarbek Meirmanov, Sergey Shmarev
Abstract:
Let
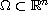 be a regular domain and
be a regular domain and
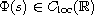 be a given function.
If
be a given function.
If
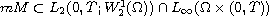 is bounded
and the set
is bounded
and the set
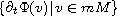 is bounded
in
is bounded
in
 ,
then there is a sequence
,
then there is a sequence
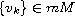 such that
such that
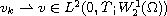 ,
and
,
and
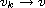 ,
,
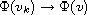 a.e. in
a.e. in
 .
This assertion is applied to prove solvability
of the one-dimensional initial and boundary-value problem for a degenerate
parabolic equation arising in the Buckley-Leverett model of two-phase filtration.
We prove existence and uniqueness of a weak solution, establish the property
of finite speed of propagation and construct a self-similar solution.
.
This assertion is applied to prove solvability
of the one-dimensional initial and boundary-value problem for a degenerate
parabolic equation arising in the Buckley-Leverett model of two-phase filtration.
We prove existence and uniqueness of a weak solution, establish the property
of finite speed of propagation and construct a self-similar solution.
Submitted September 25, 2014. Published October 27, 2014.
Math Subject Classifications: 35B27, 46E35, 76R99.
Key Words: Compactness lemma; two-phase filtration; nonlinear PDE;
degenerate parabolic equations.
Show me the PDF file (271 KB),
TEX file for this article.
 |
Anvarbek Meirmanov
Department of mahtematics,
Belgorod State University
ul.Pobedi 85, 308015 Belgorod, Russia
email: anvarbek@list.ru
|
|---|
 |
Sergey Shmarev
Department of Mathematics,
University of Oviedo
c/Calvo Sotelo s/n, 33007, Oviedo, Spain
email: shmarev@uniovi.es
|
|---|
Return to the EJDE web page
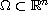 be a regular domain and
be a regular domain and
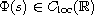 be a given function.
If
be a given function.
If
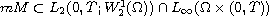 is bounded
and the set
is bounded
and the set
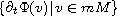 is bounded
in
is bounded
in
 ,
then there is a sequence
,
then there is a sequence
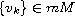 such that
such that
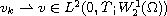 ,
and
,
and
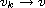 ,
,
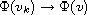 a.e. in
a.e. in
 .
This assertion is applied to prove solvability
of the one-dimensional initial and boundary-value problem for a degenerate
parabolic equation arising in the Buckley-Leverett model of two-phase filtration.
We prove existence and uniqueness of a weak solution, establish the property
of finite speed of propagation and construct a self-similar solution.
.
This assertion is applied to prove solvability
of the one-dimensional initial and boundary-value problem for a degenerate
parabolic equation arising in the Buckley-Leverett model of two-phase filtration.
We prove existence and uniqueness of a weak solution, establish the property
of finite speed of propagation and construct a self-similar solution.

