Electron. J. Diff. Equ., Vol. 2014 (2014), No. 239, pp. 1-17.

Pohozaev-type inequalities and nonexistence results for non C^2 solutions of p(x)-Laplacian equations

Gabriel Lopez

Abstract:
In this article we obtain a Pohozaev-type inequality for Sobolev spaces with variable exponents. This inequality is used for proving the nonexistence of nontrivial weak solutions for the Dirichlet problem
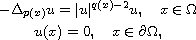
$$\displaylines{ -\Delta_{p(x)} u = |u|^{q(x)-2}u ,\quad x\in \Omega\cr u(x)=0,\quad x\in\partial\Omega, }$$
with non-standard growth. Our results extend those obtained by Otani [16].

Submitted September 6, 2014. Published November 14, 2014.
Math Subject Classifications: 35D05, 35J60, 58E05.
Key Words: Pohozaev-type inequality; p(x)-Laplace operator; Sobolev spaces with variable exponents.

Show me the PDF file (290 KB), TEX file, and other files for this article.

Gabriel López G.
Universidad Autónoma Metropolitana
México D.F., México
email: gabl@xanum.uam.mx

Return to the EJDE web page