Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 252, pp. 1-12.
Nontrivial solutions for asymmetric problems on R^N
Ruichang Pei, Jihui Zhang
Abstract:
We consider the elliptic equation
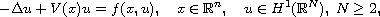
where
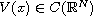 and
and
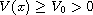 for all
for all
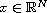 .
The nonlinear term
.
The nonlinear term
 exhibits an asymmetric growth at
exhibits an asymmetric growth at
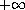 and
and
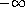 in
in
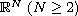 .
Namely, it is linear at
.
Namely, it is linear at
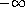 and
superlinear at
and
superlinear at
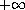 .
However, it need not satisfy the
Ambrosetti-Rabinowitz condition on the positive semiaxis. Some
existence results for nontrivial solution are established by
using the minimax methods combined with the improved
Moser-Trudinger inequality.
.
However, it need not satisfy the
Ambrosetti-Rabinowitz condition on the positive semiaxis. Some
existence results for nontrivial solution are established by
using the minimax methods combined with the improved
Moser-Trudinger inequality.
Submitted October 5, 2014. Published December 4, 2014.
Math Subject Classifications: 35J60, 35J20, 35B38.
Key Words: Schrodinger equation; asymmetric problems; one side resonance;
subcritical exponential growth.
Show me the PDF file (253 KB),
TEX file for this article.
 |
Ruichang Pei
School of Mathematics and Statistics
Tianshui Normal University
Tianshui 741001, China
email: prc211@163.com
|
|---|
 |
Jihui Zhang
School of Mathematics and Computer Sciences
Nanjing, Normal University
Nanjing 210097, China
email: zhangjihui@njnu.edu.cn
|
|---|
Return to the EJDE web page
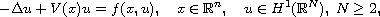
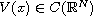 and
and
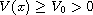 for all
for all
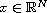 .
The nonlinear term
.
The nonlinear term
 exhibits an asymmetric growth at
exhibits an asymmetric growth at
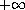 and
and
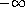 in
in
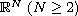 .
Namely, it is linear at
.
Namely, it is linear at
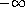 and
superlinear at
and
superlinear at
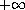 .
However, it need not satisfy the
Ambrosetti-Rabinowitz condition on the positive semiaxis. Some
existence results for nontrivial solution are established by
using the minimax methods combined with the improved
Moser-Trudinger inequality.
.
However, it need not satisfy the
Ambrosetti-Rabinowitz condition on the positive semiaxis. Some
existence results for nontrivial solution are established by
using the minimax methods combined with the improved
Moser-Trudinger inequality.

