Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 264, pp. 1-14.
Solvability of nonlinear difference equations of fourth order
Stevo Stevic, Josef Diblik, Bratislav Iricanin, Zdenek Smarda
Abstract:
In this article we show the existence of solutions to the nonlinear
difference equation
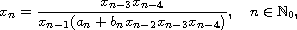
where the sequences
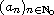 and
and
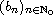 ,
and initial the values
,
and initial the values
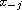 ,
,
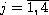 ,
are real numbers.
Also we find the set of initial values for which solutions are undefinable
when
,
are real numbers.
Also we find the set of initial values for which solutions are undefinable
when
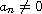 and
and
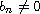 for every
for every
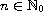 .
When these two sequences are constant, we describe the long-term behavior
of the solutions in detail.
.
When these two sequences are constant, we describe the long-term behavior
of the solutions in detail.
Submitted September 21, 2014. Published December 22, 2014.
Math Subject Classifications: 39A10, 39A20.
Key Words: Solution to difference equation; long-term behavior of solutions;
undefinable solutions.
Show me the PDF file (261 KB),
TEX file, and other files for this article.
 |
Stevo Stevic
Mathematical Institute of the Serbian Academy of Sciences
Knez Mihailova 36/III, 11000 Beograd, Serbia.
Department of Mathematics, King Abdulaziz University
P.O. Box 80203, Jeddah 21589, Saudi Arabia
email: sstevic@ptt.rs
|
|---|
 |
Josef Diblik
Department of Mathematics and Descriptive Geometry
Faculty of Civil Engineering, 60200, Brno University of Technology
Brno, Czech Republic
email: diblik.j@fce.vutbr.cz, diblik@feec.vutbr.cz
|
|---|
 |
Bratislav Iricanin
Faculty of Electrical Engineering
Belgrade University, Bulevar Kralja Aleksandra 73
11000 Beograd, Serbia
email: iricanin@etf.rs
|
|---|
 |
Zdenek Smarda
Department of Mathematics, Faculty of Electrical Engineering
and Communication
61600, Brno University of Technology
Brno, Czech Republic
email: smarda@feec.vutbr.cz
|
|---|
Return to the EJDE web page
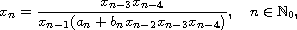
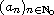 and
and
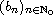 ,
and initial the values
,
and initial the values
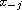 ,
,
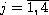 ,
are real numbers.
Also we find the set of initial values for which solutions are undefinable
when
,
are real numbers.
Also we find the set of initial values for which solutions are undefinable
when
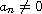 and
and
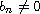 for every
for every
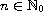 .
When these two sequences are constant, we describe the long-term behavior
of the solutions in detail.
.
When these two sequences are constant, we describe the long-term behavior
of the solutions in detail.



