We prove the existence of mild solutions for the multi-term time-fractional order abstract differential equation
![$$
D_t^{\alpha+1} u(t) + c_1 D_t^{\beta_1} u(t)+\dots +c_d {D}_t^{\beta_k} u(t)
= Au(t) + D_t^{\alpha-1} f(t,u(t)), \quad t\in [0,1],
$$](gifs/aa.gif)
with nonlocal initial conditions, where A is the generator of a strongly continuous cosine function,
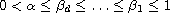and
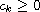for
.
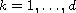Edgardo Alvarez-Pardo, Carlos Lizama
Abstract:
We prove the existence of mild solutions for the multi-term
time-fractional order abstract differential equation
with nonlocal initial conditions, where A is the generator of a
strongly continuous cosine function,
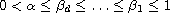and
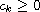for
.
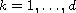Submitted August 28, 2013. Published February 5, 2014.
Math Subject Classifications: 34A08, 35R11, 47D06, 45N05.
Key Words: Multi-term time-fractional differential equation;
fractional calculus; cosine operator function; mild solution.
Show me the PDF file (236 KB), TEX file for this article.
 |
Edgardo Alvarez-Pardo Universidad del Atlántico Facultad de Ciencias Básicas, Departamento de Matemáticas Barranquilla, Colombia email: edgardoalvarez@uniatlantico.edu.co, edgalp@yahoo.com |
|---|---|
 |
Carlos Lizama Universidad de Santiago de Chile, Facultad de Ciencia Departamento de Matemática y Ciencia de la Computación Casilla 307, Correo 2, Santiago, Chile email: carlos.lizama@usach.cl |
Return to the EJDE web page