We study the boundary regularity of the solutions to inhomogeneous infinity Laplace equations. We prove that if
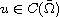 is a viscosity solution to
is a viscosity solution to
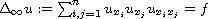 with
with
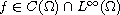 and for
and for
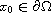 both
both
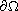 and
and
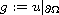 are differentiable at
are differentiable at
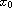 ,
then u is differentiable at
,
then u is differentiable at
 .
.
Guanghao Hong
Abstract:
We study the boundary regularity of the solutions to inhomogeneous
infinity Laplace equations. We prove that if
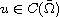 is a viscosity solution to
is a viscosity solution to
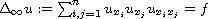 with
with
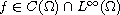 and for
and for
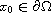 both
both
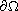 and
and
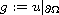 are differentiable at
are differentiable at
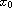 ,
then u is differentiable at
,
then u is differentiable at
 .
.
Submitted December 17, 2013. Published March 16, 2014.
Math Subject Classifications: 35J25, 35J70, 49N60.
Key Words: Boundary regularity; infinity Laplacian; comparison principle;
monotonicity.
Show me the PDF file (199 KB), TEX file, and other files for this article.
 |
Guanghao Hong School of Mathematics and Statistics Xi'an Jiaotong University Xi'an, 710049, China email: ghhongmath@gmail.com |
|---|
Return to the EJDE web page