Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 77, pp. 1-13.
Sign-changing solutions of a fourth-order elliptic equation with
supercritical exponent
Kamal Ould Bouh
Abstract:
In this article we study the nonlinear
elliptic problem involving nearly critical exponent
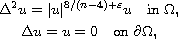
where
 is a smooth bounded domain in
is a smooth bounded domain in
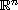 with
with
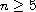 , and
, and
 is a positive parameter.
We show that, for
is a positive parameter.
We show that, for  small, there is no sign-changing solution
with low energy which blow up at exactly two points.
Moreover, we prove that this problem has no bubble-tower
sign-changing solutions.
small, there is no sign-changing solution
with low energy which blow up at exactly two points.
Moreover, we prove that this problem has no bubble-tower
sign-changing solutions.
Submitted November 15, 2013. Published March 19, 2014.
Math Subject Classifications: 35J20, 35J60.
Key Words: Sign-changing solutions; critical exponent; bubble-tower solution.
Show me the PDF file (263 KB),
TEX file for this article.
 |
Kamal Ould Bouh
Department of Mathematics
Taibah University, P.O. Box: 30002
Almadinah Almunawwarah, Saudi Arabia
email: hbouh@taibahu.edu.sa, kamal_bouh@yahoo.fr
|
|---|
Return to the EJDE web page
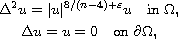
 is a smooth bounded domain in
is a smooth bounded domain in
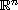 with
with
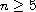 , and
, and
 is a positive parameter.
We show that, for
is a positive parameter.
We show that, for  small, there is no sign-changing solution
with low energy which blow up at exactly two points.
Moreover, we prove that this problem has no bubble-tower
sign-changing solutions.
small, there is no sign-changing solution
with low energy which blow up at exactly two points.
Moreover, we prove that this problem has no bubble-tower
sign-changing solutions.
