Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 110, pp. 1-9.
Nonexistence results for a pseudo-hyperbolic equation
in the Heisenberg group
Mokhtar Kirane, Lakhdar Ragoub
Abstract:
Sufficient conditions are obtained for the nonexistence of solutions
to the nonlinear pseudo-hyperbolic equation

where
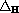 is the Kohn-Laplace operator on the
is the Kohn-Laplace operator on the
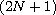 -dimensional
Heisenberg group
-dimensional
Heisenberg group
 .
Then, this result is extended to the case of a
.
Then, this result is extended to the case of a
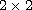 -system
of the
same type. Our technique of proof is based on judicious choices of
the test functions in the weak formulation of the sought solutions.
-system
of the
same type. Our technique of proof is based on judicious choices of
the test functions in the weak formulation of the sought solutions.
Submitted January 5, 2015. Published April 22, 2015.
Math Subject Classifications: 47J35, 34A34, 35R03.
Key Words: Nonexistence; nonlinear pseudo-hyperbolic equation;
systems of pseudo-hyperbolic equations; Heisenberg group.
Show me the PDF file (211 KB),
TEX file for this article.
 |
Mokhtar Kirane
Laboratoire de Mathématiques, Image et Applications
Pôle Sciences et Technologies
Université de La Rochelle
Avenue M. Crépeau, 17042 La Rochelle, France
email: mkirane@univ-lr.fr
|
|---|
 |
Lakhdar Ragoub
Al Yamamah University
College of Computers and Information Systems
P.O. Box 45180, Riyadh 11512, Saudi Arabia
email: l_ragoub@yu.edu.sa
|
|---|
Return to the EJDE web page

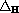 is the Kohn-Laplace operator on the
is the Kohn-Laplace operator on the
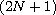 -dimensional
Heisenberg group
-dimensional
Heisenberg group
 .
Then, this result is extended to the case of a
.
Then, this result is extended to the case of a
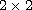 -system
of the
same type. Our technique of proof is based on judicious choices of
the test functions in the weak formulation of the sought solutions.
-system
of the
same type. Our technique of proof is based on judicious choices of
the test functions in the weak formulation of the sought solutions.

