Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 12, pp. 1-11.
Gradient estimates for a nonlinear parabolic equation
with potential under geometric flow
Abimbola Abolarinwa
Abstract:
Let (M,g) be an n dimensional complete Riemannian manifold.
In this article we prove local Li-Yau type gradient estimates for all positive
solutions to the nonlinear parabolic equation
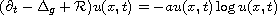
along the generalised geometric flow on M. Here
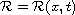 is a smooth potential function and a
is an arbitrary constant. As an application we derive a global estimate and
a space-time Harnack inequality.
is a smooth potential function and a
is an arbitrary constant. As an application we derive a global estimate and
a space-time Harnack inequality.
Submitted December 8, 2014. Published January 8, 2015.
Math Subject Classifications: 35K55, 53C21, 53C44, 58J35.
Key Words: Gradient estimates; Harnack inequalities; parabolic equations;
geometric flows.
Show me the PDF file (232 KB),
TEX file for this article.
 |
Abimbola Abolarinwa
Department of Mathematics, University of Sussex
Brighton, BN1 9QH, United Kingdom
email: A.Abolarinwa@sussex.ac.uk
|
|---|
Return to the EJDE web page
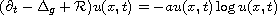
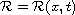 is a smooth potential function and a
is an arbitrary constant. As an application we derive a global estimate and
a space-time Harnack inequality.
is a smooth potential function and a
is an arbitrary constant. As an application we derive a global estimate and
a space-time Harnack inequality.
