Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 161, pp. 1-16.
Extremal points for a higher-order fractional boundary-value problem
Aijun Yang, Johnny Henderson, Charles Nelms Jr.
Abstract:
The Krein-Rutman theorem is applied to establish the extremal point,
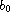 ,
for a higher-order Riemann-Liouville fractional equation,
,
for a higher-order Riemann-Liouville fractional equation,
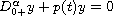 ,
,
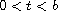 ,
,
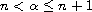 ,
,
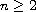 ,
under the boundary conditions
,
under the boundary conditions
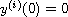 ,
,
 ,
,
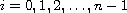 .
The key argument is that a mapping,
which maps a linear, compact operator, depending on
.
The key argument is that a mapping,
which maps a linear, compact operator, depending on
 to its spectral radius,
is continuous and strictly increasing as a function of b.
Furthermore, we also treat a nonlinear problem as an application of the
result for the extremal point for the linear case.
to its spectral radius,
is continuous and strictly increasing as a function of b.
Furthermore, we also treat a nonlinear problem as an application of the
result for the extremal point for the linear case.
Submitted May 19, 2015. Published June 16, 2015.
Math Subject Classifications: 26A33, 34B08, 34B40.
Key Words: u-positive operator; fractional boundary value problem;
spectral radius
Show me the PDF file (257 KB),
TEX file for this article.
 |
Aijun Yang
Zhejiang University of Technology
College of Science
Hangzhou 310023, China
email: yangaij2004@163.com, Aijun_Yang@baylor.edu
|
|---|
 |
Johnny Henderson
Department of Mathematics, Baylor University
Waco, TX 76798-7328, USA
email: Johnny_Henderson@baylor.edu
|
|---|
| |
Charles Nelms Jr.
Department of Mathematics, Baylor University,
Waco, TX 76798-7328, USA
email: Charles_Nelms@baylor.edu
|
|---|
Return to the EJDE web page
 ,
for a higher-order Riemann-Liouville fractional equation,
,
for a higher-order Riemann-Liouville fractional equation,
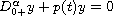 ,
,
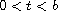 ,
,
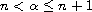 ,
,
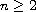 ,
under the boundary conditions
,
under the boundary conditions
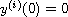 ,
,
 ,
,
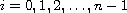 .
The key argument is that a mapping,
which maps a linear, compact operator, depending on
.
The key argument is that a mapping,
which maps a linear, compact operator, depending on
 to its spectral radius,
is continuous and strictly increasing as a function of b.
Furthermore, we also treat a nonlinear problem as an application of the
result for the extremal point for the linear case.
to its spectral radius,
is continuous and strictly increasing as a function of b.
Furthermore, we also treat a nonlinear problem as an application of the
result for the extremal point for the linear case.

