Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 162, pp. 1-14.
Estimates for damped fractional wave equations and applications
Jiecheng Chen, Dashan Fan, Chunjie Zhang
Abstract:
In our previous article [1] we estimated the
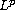 -norm
(
-norm
(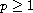 ) of the
solution to damped fractional wave equation. In this article,
we prove other
) of the
solution to damped fractional wave equation. In this article,
we prove other 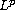 estimates, with some emphasis on requiring less
regularity of the initial data. We also study the Strichartz type estimate
of this equation. Finally we present some application of these estimates,
for proving existence of global solutions to semilinear damped fractional
wave equations.
estimates, with some emphasis on requiring less
regularity of the initial data. We also study the Strichartz type estimate
of this equation. Finally we present some application of these estimates,
for proving existence of global solutions to semilinear damped fractional
wave equations.
Submitted November 30, 2014. Published June 16, 2015.
Math Subject Classifications: 35L05, 46E35, 42B37.
Key Words: Damped fractional wave equation;
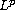 -estimate;
Strichartz estimate.
-estimate;
Strichartz estimate.
Show me the PDF file (263 KB),
TEX file for this article.
 |
Jiecheng Chen
Department of Mathematics
Zhejiang Normal University
Jinhua 321004, China
email: jcchen@zjnu.edu.cn
|
|---|
 |
Dashan Fan
Department of Mathematics
University of Wisconsin
Milwaukee, WI 53201, USA
email: fan@uwm.edu
|
|---|
 |
Chunjie Zhang
Department of Mathematics
Hangzhou Dianzi University
Hangzhou 310018, China
email: purezhang@hdu.edu.cn
|
|---|
Return to the EJDE web page
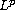 -norm
(
-norm
(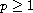 ) of the
solution to damped fractional wave equation. In this article,
we prove other
) of the
solution to damped fractional wave equation. In this article,
we prove other 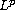 estimates, with some emphasis on requiring less
regularity of the initial data. We also study the Strichartz type estimate
of this equation. Finally we present some application of these estimates,
for proving existence of global solutions to semilinear damped fractional
wave equations.
estimates, with some emphasis on requiring less
regularity of the initial data. We also study the Strichartz type estimate
of this equation. Finally we present some application of these estimates,
for proving existence of global solutions to semilinear damped fractional
wave equations.


