In this article, we consider the tridimensional generalized Hall magneto-hydrodynamics (Hall-MHD) system, with
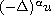 and
and
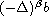 .
For
.
For
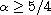 ,
,
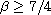 ,
we obtain the global regularity of classical solutions.
For
,
we obtain the global regularity of classical solutions.
For
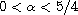 and
and
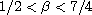 ,
with small data,
the system also possesses global classical solutions. In addition,
for the standard Hall-MHD system,
,
with small data,
the system also possesses global classical solutions. In addition,
for the standard Hall-MHD system,
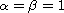 ,
by adding a suitable condition, we give a positive answer to the open
question in [3].
At last, we study the regularity criterions of generalized Hall-MHD system.
In particular, we prove the regularity criterion in terms of horizontal
gradient
,
by adding a suitable condition, we give a positive answer to the open
question in [3].
At last, we study the regularity criterions of generalized Hall-MHD system.
In particular, we prove the regularity criterion in terms of horizontal
gradient
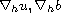 for
for
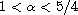 ,
,
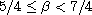 .
.
