Electron. J. Diff. Equ., Vol. 2015 (2015), No. 182, pp. 1-7.

A Liouville type theorem for p-Laplace equations

Cristian Enache

Abstract:
In this note we study solutions defined on the whole space 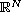$\mathbb{R}^N$ for the p-Laplace equation
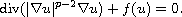
$$ \hbox{div}(| \nabla u|^{p-2}\nabla u)+f(u)=0. $$
Under an appropriate condition on the growth of f, which is weaker than conditions previously considered in McCoy [3] and Cuccu-Mhammed-Porru [1], we prove the non-existence of non-trivial positive solutions.

Submitted October 18, 2014. Published July 1, 2015.
Math Subject Classifications: 70H25.
Key Words: p-Laplace equation; Liouville theorem; entire solutions.

Show me the PDF file (184 KB), TEX file for this article.

Cristian Enache
Simion Stoilow Institute of Mathematics
of the Romanian Academy 010702
Bucharest, Romania
email: cenache23@yahoo.com

Return to the EJDE web page