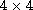 matrices
matrices
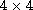 matrices
matrices
Jeremy Mandelkern
Abstract:
In Coddington and Levison [7, p. 119, Thm. 4.1] and
Balser [4, p. 18-19, Thm. 5], matrix formulations of Frobenius
theory, near a regular singular point, are given using
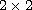 matrix
recurrence relations yielding fundamental matrices consisting of two
linearly independent solutions together with their quasi-derivatives.
In this article we apply a reformulation of these matrix methods to the
Bessel equation of nonintegral order. The reformulated approach of this
article differs from [7] and [4] by its
implementation of a new ``vectorization'' procedure that yields recurrence
relations of an altogether different form: namely, it replaces the implicit
matrix
recurrence relations yielding fundamental matrices consisting of two
linearly independent solutions together with their quasi-derivatives.
In this article we apply a reformulation of these matrix methods to the
Bessel equation of nonintegral order. The reformulated approach of this
article differs from [7] and [4] by its
implementation of a new ``vectorization'' procedure that yields recurrence
relations of an altogether different form: namely, it replaces the implicit
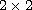 matrix recurrence relations of both [7] and
[4] by explicit
matrix recurrence relations of both [7] and
[4] by explicit
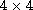 matrix recurrence relations
that are implemented by means only of
matrix recurrence relations
that are implemented by means only of
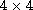 matrix products.
This new idea of using a vectorization procedure may further enable the
development of symbolic manipulator programs for matrix forms of the
Frobenius theory.
matrix products.
This new idea of using a vectorization procedure may further enable the
development of symbolic manipulator programs for matrix forms of the
Frobenius theory.
Submitted January 12, 2015. Published August 17, 2015.
Math Subject Classifications: 34B30, 33C10, 68W30, 34-03, 01A55.
Key Words: Matrix power series; Frobenius theory; Bessel equation.
An addendum was posted on May 11, 2017, It modifies two matrices from Section 7. See the last page of this article.
Show me the PDF file (284 KB), TEX file for this article.
 |
Jeremy Mandelkern Department of Mathematics Eastern Florida State College Melbourne, FL 32935, USA email: mandelkernj@easternflorida.edu |
|---|
Return to the EJDE web page