Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 287, pp. 1-32.
Holder continuity of bounded weak solutions to generalized parabolic
p-Laplacian equations I: degenerate case
Sukjung Hwang, Gary M. Lieberman
Abstract:
Here we generalize quasilinear parabolic p-Laplacian type equations to
obtain the prototype equation
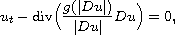
where g is a nonnegative, increasing, and continuous function trapped
in between two power functions
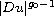 and
and
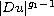 with
with
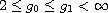 .
Through this generalization in
the setting from Orlicz spaces, we provide a proof for the Holder
continuity of such solutions which has much in common with that proof
of Holder continuity of solutions of singular equations.
.
Through this generalization in
the setting from Orlicz spaces, we provide a proof for the Holder
continuity of such solutions which has much in common with that proof
of Holder continuity of solutions of singular equations.
Submitted July 17, 2015. Published November 19, 2015.
Math Subject Classifications: 35B45, 35K65.
Key Words: Quasilinear parabolic equation; degenerate equation;
generalized structure; a priori estimate; Holder continuity.
Show me the PDF file (399 KB),
TEX file for this article.
 |
Sukjung Hwang
Center for Mathematical Analysis and Computation
Yonsei University, Seoul 03722, Korea
email: sukjung_hwang@yonsei.ac.kr
|
|---|
 |
Gary M. Lieberman
Department of Mathematics
Iowa State University
Ames, IA 50011, USA
email: lieb@iastate.edu
|
|---|
Return to the EJDE web page
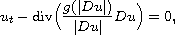
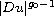 and
and
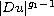 with
with
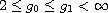 .
Through this generalization in
the setting from Orlicz spaces, we provide a proof for the Holder
continuity of such solutions which has much in common with that proof
of Holder continuity of solutions of singular equations.
.
Through this generalization in
the setting from Orlicz spaces, we provide a proof for the Holder
continuity of such solutions which has much in common with that proof
of Holder continuity of solutions of singular equations.

