Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 42, pp. 1-21.
Favard spaces and admissibility for Volterra systems with scalar kernel
Hamid Bounit, Ahmed Fadili
Abstract:
We introduce the Favard spaces for resolvent families, extending some
well-known theorems for semigroups. Furthermore, we show the relationship
between these Favard spaces and the
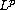 -admissibility
of control
operators for scalar Volterra linear systems in Banach spaces, extending
some results in [22]. Assuming that the kernel a(t) is
a creep function which satisfies
-admissibility
of control
operators for scalar Volterra linear systems in Banach spaces, extending
some results in [22]. Assuming that the kernel a(t) is
a creep function which satisfies
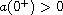 ,
we prove an analogue
version of the Weiss conjecture for scalar Volterra linear systems
when p=1. To this end, we also show that the finite-time and infinite-time
(resp. finite-time and uniform finite-time)
,
we prove an analogue
version of the Weiss conjecture for scalar Volterra linear systems
when p=1. To this end, we also show that the finite-time and infinite-time
(resp. finite-time and uniform finite-time)
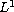 -admissibility
coincide for exponentially stable resolvent families (reps. for reflexive
state space), extending well-known results for semigroups.
-admissibility
coincide for exponentially stable resolvent families (reps. for reflexive
state space), extending well-known results for semigroups.
Submitted March 22, 2014. Published February 12, 2015.
Math Subject Classifications: 45D05, 45E05, 45E10, 47D06.
Key Words: Semigroups; Volterra integral equations; resolvent family;
Favard space; admissibility.
Show me the PDF file (327 KB),
TEX file, and other files for this article.
| |
Hamid Bounit
Department of Mathematics, Faculty of Sciences
Ibn Zohr University, BP 8106
Agadir 80 000, Morocco
email: h.bounit@uiz.ac.ma
|
|---|
 |
Ahmed Fadili
Department of Mathematics, Faculty of Sciences
Ibn Zohr University, BP 8106
Agadir 80 000, Morocco
email: ahmed.fadili@edu.uiz.ac.ma
|
|---|
Return to the EJDE web page
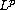 -admissibility
of control
operators for scalar Volterra linear systems in Banach spaces, extending
some results in [22]. Assuming that the kernel a(t) is
a creep function which satisfies
-admissibility
of control
operators for scalar Volterra linear systems in Banach spaces, extending
some results in [22]. Assuming that the kernel a(t) is
a creep function which satisfies
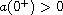 ,
we prove an analogue
version of the Weiss conjecture for scalar Volterra linear systems
when p=1. To this end, we also show that the finite-time and infinite-time
(resp. finite-time and uniform finite-time)
,
we prove an analogue
version of the Weiss conjecture for scalar Volterra linear systems
when p=1. To this end, we also show that the finite-time and infinite-time
(resp. finite-time and uniform finite-time)
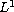 -admissibility
coincide for exponentially stable resolvent families (reps. for reflexive
state space), extending well-known results for semigroups.
-admissibility
coincide for exponentially stable resolvent families (reps. for reflexive
state space), extending well-known results for semigroups.
