Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 51, pp. 1-5.
Nonexistence of soliton-like solutions for defocusing
generalized KdV equations
Soonsik Kwon, Shuanglin Shao
Abstract:
We consider the global dynamics of the defocusing generalized KdV equation
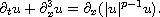
We use Tao's theorem [5] that the energy moves faster than the
mass to prove a moment type dispersion estimate. As an application of
the dispersion estimate, we show that there is no soliton-like solutions
with a certain decaying assumption.
Submitted May 21, 2013. Published February 24, 2015.
Math Subject Classifications: 35Q53.
Key Words: Generalized KdV equation; soliton, scattering.
Show me the PDF file (181 KB),
TEX file for this article.
 |
Soonsik Kwon
Department of Mathematical Sciences
Korea Advanced Institute of Science and Technology
291 Daehak-ro Yuseong-gu, Daejeon 305-701, Korea
email: soonsikk@kaist.edu
|
|---|
 |
Shuanglin Shao
Department of Mathematics, University of Kansas
Lawrence, KS 66045, USA
email: slshao@math.ku.edu
|
|---|
Return to the EJDE web page