Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 57, pp. 1-33.
Existence and asymptotic behavior of a unique solution to a
singular Dirichlet boundary-value problem with a convection term
Haitao Wan
Abstract:
In this article, we consider the problem
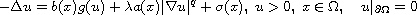
with
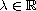 ,
,
![$q\in [0, 2]$](gifs/ac.gif) in a smooth bounded domain
in a smooth bounded domain
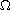 of
of
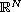 .
The weight functions
.
The weight functions
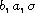 belong to
belong to
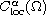 satisfying
satisfying
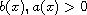 ,
,
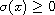 ,
,
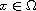 ,
which may vanish or
be singular on the boundary.
,
which may vanish or
be singular on the boundary.
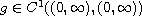 satisfies
satisfies
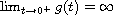 . Our results
include the existence, uniqueness and the exact boundary asymptotic
behavior and global asymptotic behavior of the solution.
. Our results
include the existence, uniqueness and the exact boundary asymptotic
behavior and global asymptotic behavior of the solution.
Submitted December 9, 2014. Published March 6, 2015.
Math Subject Classifications: 35A01, 35B40, 35J25.
Key Words: Singular Dirichlet problem; Karamata regular variation theory;
convection term; boundary asymptotic behavior; global asymptotic behavior.
Show me the PDF file (430 KB),
TEX file for this article.
 |
Haitao Wan
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: wht200805@163.com, Phone: +8618954556896
|
|---|
Return to the EJDE web page
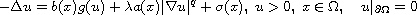
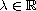 ,
,
![$q\in [0, 2]$](gifs/ac.gif) in a smooth bounded domain
in a smooth bounded domain
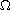 of
of
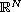 .
The weight functions
.
The weight functions
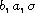 belong to
belong to
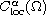 satisfying
satisfying
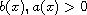 ,
,
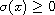 ,
,
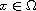 ,
which may vanish or
be singular on the boundary.
,
which may vanish or
be singular on the boundary.
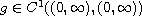 satisfies
satisfies
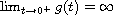 . Our results
include the existence, uniqueness and the exact boundary asymptotic
behavior and global asymptotic behavior of the solution.
. Our results
include the existence, uniqueness and the exact boundary asymptotic
behavior and global asymptotic behavior of the solution.
