We consider the quasi-periodic cocycles
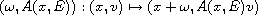 with
with
 Diophantine. Let
Diophantine. Let
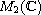 be a normed space endowed with the
matrix norm, whose elements are the
be a normed space endowed with the
matrix norm, whose elements are the
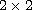 matrices.
Assume that
matrices.
Assume that
 is jointly continuous,
depends analytically on
is jointly continuous,
depends analytically on
 and is Holder continuous in
and is Holder continuous in
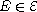 ,
where
,
where
 is a compact metric space and
is a compact metric space and
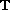 is the torus. We prove that if two Lyapunov
exponents are distinct at one point
is the torus. We prove that if two Lyapunov
exponents are distinct at one point
 ,
then these two
Lyapunov exponents are Holder continuous at any E in a ball
central at
,
then these two
Lyapunov exponents are Holder continuous at any E in a ball
central at
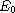 .
Moreover, we will give the expressions of the radius
of this ball and the Holder exponents of the two Lyapunov exponents.
.
Moreover, we will give the expressions of the radius
of this ball and the Holder exponents of the two Lyapunov exponents.
