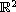
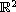
Yibin Zhang, Haitao Yang
Abstract:
Let
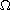 be a bounded domain in
be a bounded domain in
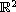 with smooth
boundary and
with smooth
boundary and
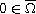 ,
we study the Neumann problem
for the Henon equation
,
we study the Neumann problem
for the Henon equation

where
 denotes the outer unit normal vector to
denotes the outer unit normal vector to
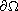 ,
,
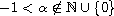 and p is a large exponent.
In a constructive way, we show that, as p approaches
and p is a large exponent.
In a constructive way, we show that, as p approaches
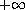 ,
such a problem has a family of positive solutions with arbitrarily
many interior and boundary spikes involving the origin.
The same techniques lead also to a more general result on
Henon-type weights.
,
such a problem has a family of positive solutions with arbitrarily
many interior and boundary spikes involving the origin.
The same techniques lead also to a more general result on
Henon-type weights.
Submitted October 14, 2014. Published March 26, 2015.
Math Subject Classifications: 35J25, 35J20, 58K05.
Key Words: Mixed interior and boundary peak solutions; Henon-type weight;
large exponent; Lyapunov-Schmidt reduction process.
Show me the PDF file (404 KB), TEX file, and other files for this article.
 |
Yibin Zhang College of Sciences, Nanjing Agricultural University Nanjing 210095, China email: yibin10201029@njau.edu.cn |
|---|---|
| Haitao Yang Department of Mathematics, Zhejiang University Hangzhou 310027, China email: htyang@css.zju.edu.cn |
Return to the EJDE web page