The main goal in this article is to justify that source-type and other global-in-time similarity solutions of the Cauchy problem for the fourth-order thin film equation
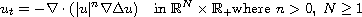
can be obtained by a continuous deformation (a homotopy path) as
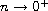 .
This is done by reducing to similarity solutions
(given by eigenfunctions of a rescaled linear operator
.
This is done by reducing to similarity solutions
(given by eigenfunctions of a rescaled linear operator
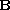 )
of the classic bi-harmonic equation
)
of the classic bi-harmonic equation

This approach leads to a countable family of various global similarity patterns of the thin film equation, and describes their oscillatory sign-changing behav iour by using the known asymptotic properties of the fundamental solution of bi-harmonic equation. The branching from
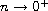 for thin film equation requires Hermitian spectral
theory for a pair
for thin film equation requires Hermitian spectral
theory for a pair
 of non-self adjoint operators
and leads to a number of difficult mathematical problems. These include, as
a key part, the problem of multiplicity of solutions, which is under
particular scrutiny.
of non-self adjoint operators
and leads to a number of difficult mathematical problems. These include, as
a key part, the problem of multiplicity of solutions, which is under
particular scrutiny.

