Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 103, pp. 1-21.
Multi-peak solutions for a planar Robin nonlinear
elliptic problem with large exponent
Yibin Zhang, Lei Shi
Abstract:
We consider the elliptic equation
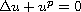 in a bounded smooth domain
in a bounded smooth domain
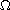 in
in
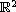 subject to the Robin boundary condition
subject to the Robin boundary condition
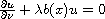 .
Here
.
Here
 denotes the unit outward normal vector on
denotes the unit outward normal vector on
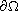 ,
,
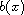 is a smooth positive function defined on
is a smooth positive function defined on
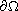 ,
,
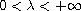 ,
and p is a large exponent.
For any fixed
,
and p is a large exponent.
For any fixed
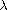 large we find topological conditions on
large we find topological conditions on
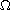 which ensure the existence of
a positive solution with exactly m peaks separated by a
uniform positive distance from the boundary and each from other
as
which ensure the existence of
a positive solution with exactly m peaks separated by a
uniform positive distance from the boundary and each from other
as
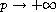 and
and
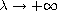 .
In particular,
for a nonsimply connected domain such solution exists for any
.
In particular,
for a nonsimply connected domain such solution exists for any
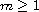 .
.
Submitted November 26, 2015. Published April 21, 2016.
Math Subject Classifications: 35J25, 35B25, 35B38.
Key Words: Concentrating solutions; large exponent; Robin boundary condition;
finite-dimensional reduction.
Show me the PDF file (329 KB),
TEX file for this article.
 |
Yibin Zhang
College of Sciences
Nanjing Agricultural University
Nanjing 210095, China
email: yibin10201029@njau.edu.cn
|
|---|
| |
Lei Shi
College of Sciences
Nanjing Agricultural University
Nanjing 210095, China
email: shileijsxh@163.com
|
|---|
Return to the EJDE web page
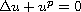 in a bounded smooth domain
in a bounded smooth domain
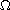 in
in
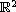 subject to the Robin boundary condition
subject to the Robin boundary condition
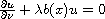 .
Here
.
Here
 denotes the unit outward normal vector on
denotes the unit outward normal vector on
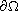 ,
,
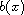 is a smooth positive function defined on
is a smooth positive function defined on
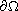 ,
,
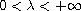 ,
and p is a large exponent.
For any fixed
,
and p is a large exponent.
For any fixed
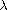 large we find topological conditions on
large we find topological conditions on
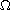 which ensure the existence of
a positive solution with exactly m peaks separated by a
uniform positive distance from the boundary and each from other
as
which ensure the existence of
a positive solution with exactly m peaks separated by a
uniform positive distance from the boundary and each from other
as
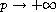 and
and
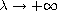 .
In particular,
for a nonsimply connected domain such solution exists for any
.
In particular,
for a nonsimply connected domain such solution exists for any
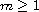 .
.
