Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 136, pp. 1-16.
Quenching phenomenon of singular parabolic problems with L^1 initial data
Anh Nguyen Dao, Jesus Ildefonso Diaz, Paul Sauvy
Abstract:
We extend some previous existence results for quenching type parabolic
problems involving a negative power of the unknown in the equation
to the case of merely integrable initial data. We show that
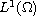 is the suitable framework to obtain the continuous
dependence with respect to some norm of the initial datum;
This way we answer to the question raised by several authors in
the previous literature. We also show the complete quenching phenomena
for such a L^1-initial datum.
is the suitable framework to obtain the continuous
dependence with respect to some norm of the initial datum;
This way we answer to the question raised by several authors in
the previous literature. We also show the complete quenching phenomena
for such a L^1-initial datum.
Submitted January 15, 2016. Published June 8, 2016.
Math Subject Classifications: 35K55, 35K67, 35K65.
Key Words: Quenching type parabolic equations;
L^1-initial datum; free boundary.
Show me the PDF file (288 KB),
TEX file for this article.
| |
Anh Nguyen Dao
Faculty of Mathematics and Statistics
Ton Duc Thang University, Ho Chi Minh City, Vietnam
email: daonguyenanh@tdt.edu.vn
|
|---|
 |
Jesús Ildefonso Díaz
Instituto de Matemática Interdisciplinar
Universidad Complutense de Madrid
28040 Madrid, Spain
email: ildefonso.diaz@mat.ucm.es
|
|---|
 |
Paul Sauvy
Institut Mathèmatique de Toulouse
Université Toulouse 1
31000 Toulouse France
email: paul.sauvy@ut-capitole.fr
|
|---|
Return to the EJDE web page
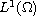 is the suitable framework to obtain the continuous
dependence with respect to some norm of the initial datum;
This way we answer to the question raised by several authors in
the previous literature. We also show the complete quenching phenomena
for such a L^1-initial datum.
is the suitable framework to obtain the continuous
dependence with respect to some norm of the initial datum;
This way we answer to the question raised by several authors in
the previous literature. We also show the complete quenching phenomena
for such a L^1-initial datum.

