Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 137, pp. 1-7.
Logarithmically improved regularity criteria for supercritical
quasi-geostrophic equations in Orlicz-Morrey spaces
Sadek Gala, Maria Alessandra Ragusa
Abstract:
This article provides a regularity criterion for the surface quasi-geostrophic
equation with supercritical dissipation. This criterion is in terms of the
norm of the solution in a Orlicz-Morrey space.
The result shows that, if a weak solutions
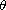 satisfies
satisfies

for some
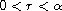 and
and
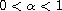 ,
then
,
then
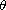 is regular at t=T. In view of the embedding
is regular at t=T. In view of the embedding
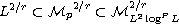 with
with
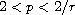 and P>1, our result extends the results
due to Xiang [29] and Jia-Dong [15].
and P>1, our result extends the results
due to Xiang [29] and Jia-Dong [15].
Submitted September 28, 2015. Published June 8, 2016.
Math Subject Classifications: 35Q35, 76D03.
Key Words: Quasi-geostrophic equations; logarithmical regularity criterion;
Orlicz-Morrey space.
Show me the PDF file (225 KB),
TEX file for this article.
Sadek Gala
Department of Mathematics
University of Mostaganem, Box 227
Mostaganem 27000, Algeria
email: sadek.gala@gmail.com
|
Maria Alessandra Ragusa
Dipartimento di Matematica e Informatica
Università di Catania
Viale Andrea Doria, 6 95125 Catania, Italy
email: maragusa@dmi.unict.it
|
Return to the EJDE web page
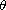 satisfies
satisfies

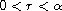 and
and
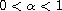 ,
then
,
then
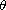 is regular at t=T. In view of the embedding
is regular at t=T. In view of the embedding
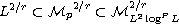 with
with
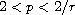 and P>1, our result extends the results
due to Xiang [29] and Jia-Dong [15].
and P>1, our result extends the results
due to Xiang [29] and Jia-Dong [15].