Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 157, pp. 1-13.
Existence of solutions to Burgers equations in domains
that can be transformed into rectangles
Yassine Benia, Boubaker-Khaled Sadallah
Abstract:
This work is concerned with Burgers equation
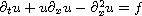 (with Dirichlet boundary conditions) in the
non rectangular domain
(with Dirichlet boundary conditions) in the
non rectangular domain
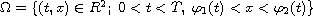 (where
(where
 for all
for all
![$t\in [ 0;T]$](gifs/ad.gif) ).
This domain will be transformed into a rectangle by a regular change of
variables. The right-hand side lies in the Lebesgue space
).
This domain will be transformed into a rectangle by a regular change of
variables. The right-hand side lies in the Lebesgue space
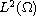 ,
and the initial condition is in the usual Sobolev space
,
and the initial condition is in the usual Sobolev space
 .
Our goal is to establish the existence, uniqueness and the optimal regularity
of the solution in the anisotropic Sobolev space.
.
Our goal is to establish the existence, uniqueness and the optimal regularity
of the solution in the anisotropic Sobolev space.
Submitted April 15, 2016. Published June 21, 2016.
Math Subject Classifications: 35K58, 35Q35.
Key Words: Semilinear parabolic problem; Burgers equation; existence;
uniqueness; anisotropic Sobolev space.
Show me the PDF file (249 KB),
TEX file for this article.
 |
Yassine Benia
Department of Mathematics
University of Tiaret, B.P. 78
14000, Tiaret, Algeria
email: benia.yacine@yahoo.fr
|
|---|
 |
Boubaker-Khaled Sadallah
Lab. PDE and Hist Maths
Dept of Mathematics, E.N.S.
16050, Kouba, Algiers, Algeria
email: sadallah@ens-kouba.dz
|
|---|
Return to the EJDE web page
 (with Dirichlet boundary conditions) in the
non rectangular domain
(with Dirichlet boundary conditions) in the
non rectangular domain
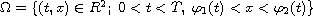 (where
(where
 for all
for all
![$t\in [ 0;T]$](gifs/ad.gif) ).
This domain will be transformed into a rectangle by a regular change of
variables. The right-hand side lies in the Lebesgue space
).
This domain will be transformed into a rectangle by a regular change of
variables. The right-hand side lies in the Lebesgue space
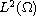 ,
and the initial condition is in the usual Sobolev space
,
and the initial condition is in the usual Sobolev space
 .
Our goal is to establish the existence, uniqueness and the optimal regularity
of the solution in the anisotropic Sobolev space.
.
Our goal is to establish the existence, uniqueness and the optimal regularity
of the solution in the anisotropic Sobolev space.

