Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 196, pp. 1-22.
Stable solutions for equations with a quadratic gradient term
Joana Terra
Abstract:
We consider positive solutions to the non-variational family of equations
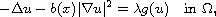
where
 ,
b(x) is a given function, g is an increasing
nonlinearity with g(0)> 0 and
,
b(x) is a given function, g is an increasing
nonlinearity with g(0)> 0 and
 is a bounded smooth domain.
We introduce the definition of stability for non-variational problems and
establish existence and regularity results for stable solutions.
These results generalize the classical results obtained when
is a bounded smooth domain.
We introduce the definition of stability for non-variational problems and
establish existence and regularity results for stable solutions.
These results generalize the classical results obtained when
 is a constant function making the problem variational after a suitable
transformation.
is a constant function making the problem variational after a suitable
transformation.
Submitted July 30, 2015. Published July 21, 2016.
Math Subject Classifications: 35B35, 35J61.
Key Words: Non-variational problem; stable solution.
Show me the PDF file (311 KB),
TEX file for this article.
 |
Joana Terra
Departamento de Matemática, FCEyN
and IMAS-CONICET, UBA (1428)
Buenos Aires, Argentina
email: joanamterra@gmail.com
|
|---|
Return to the EJDE web page
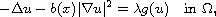
 ,
b(x) is a given function, g is an increasing
nonlinearity with g(0)> 0 and
,
b(x) is a given function, g is an increasing
nonlinearity with g(0)> 0 and
 is a bounded smooth domain.
We introduce the definition of stability for non-variational problems and
establish existence and regularity results for stable solutions.
These results generalize the classical results obtained when
is a bounded smooth domain.
We introduce the definition of stability for non-variational problems and
establish existence and regularity results for stable solutions.
These results generalize the classical results obtained when
 is a constant function making the problem variational after a suitable
transformation.
is a constant function making the problem variational after a suitable
transformation.
