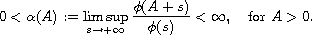Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 206, pp. 1-17.
Existence of solutions for p-Laplacian-like differential equation with
multi-point nonlinear Neumann boundary conditions at resonance
Le Xuan Truong, Le Cong Nhan
Abstract:
This work concerns the multi-point nonlinear Neumann boundary-value
problem involving a p-Laplacian-like operator
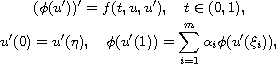
where
 is an odd increasing homeomorphism
with
is an odd increasing homeomorphism
with
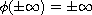 such that
such that
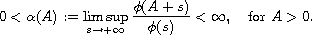
By using an extension of Mawhin's continuation theorem, we establish
sufficient conditions for the existence of at least one solution.
Submitted December 24, 2014. Published July 29, 2016.
Math Subject Classifications: 34B10, 34B15.
Key Words: Continuation theorem; p-Laplacian differential equation; resonance.
Show me the PDF file (281 KB),
TEX file for this article.
 |
Le Xuan Truong
Division of Computational Mathematics and Engineering
Institute for Computational Science
Ton Duc Thang University
Ho Chi Minh City, Vietnam
email: lexuantruong@tdt.edu.vn
|
|---|
 |
Le Cong Nhan
Mathematic Department
An Giang University
18 Ung Van Khiem Str, An Giang, Vietnam
email: lcnhanmathagu@gmail.com
|
|---|
Return to the EJDE web page
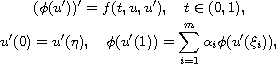
 is an odd increasing homeomorphism
with
is an odd increasing homeomorphism
with
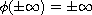 such that
such that