Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 223, pp. 1-14.
Existence and behavior of positive solutions to
elliptic system with Hardy potential
Lei Wei, Xiyou Cheng, Zhaosheng Feng
Abstract:
In this article, we study a class of elliptic systems with Hardy potentials.
We analyze the possible behavior of radial solutions to the system when
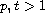 ,
,
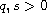 and
and
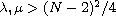 ,
and obtain the existence of positive solutions to the system with the
Dirichlet boundary condition under certain conditions.
When
,
and obtain the existence of positive solutions to the system with the
Dirichlet boundary condition under certain conditions.
When
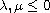 ,
p,t>1
and
q,s>0,
we show that any radial
positive solution is decreasing in r.
,
p,t>1
and
q,s>0,
we show that any radial
positive solution is decreasing in r.
Submitted January 12, 2016. Published August 17, 2016.
Math Subject Classifications: 35B40, 35J25.
Key Words: Elliptic system; Hardy potential; existence; positive solution;
blow up.
Show me the PDF file (264 KB),
TEX file for this article.
 |
Lei Wei
School of Mathematics and Statistics
Jiangsu Normal University
Xuzhou 221116, China
email: wlxznu@163.com
|
|---|
| |
Xiyou Cheng
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: chengxy@lzu.edu.cn
|
|---|
 |
Zhaosheng Feng
Department of Mathematics
University of Texas-Rio Grande Valley
Edinburg, TX 78539, USA
email: zhaosheng.feng@utrgv.edu
|
|---|
Return to the EJDE web page
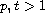 ,
,
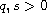 and
and
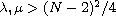 ,
and obtain the existence of positive solutions to the system with the
Dirichlet boundary condition under certain conditions.
When
,
and obtain the existence of positive solutions to the system with the
Dirichlet boundary condition under certain conditions.
When
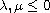 ,
p,t>1
and
q,s>0,
we show that any radial
positive solution is decreasing in r.
,
p,t>1
and
q,s>0,
we show that any radial
positive solution is decreasing in r.

