Electron. J. Differential Equations, Vol. 2016 (2016), No. 255, pp. 1-20.

Stability analysis and Hopf bifurcation of density-dependent predator-prey systems with Beddington-DeAngelis functional response

Xin Jiang, Zhikun She, Zhaosheng Feng

Abstract:
In this article, we study a density-dependent predator-prey system with the Beddington-DeAngelis functional response for stability and Hopf bifurcation under certain parametric conditions. We start with the condition of the existence of the unique positive equilibrium, and provide two sufficient conditions for its local stability by the Lyapunov function method and the Routh-Hurwitz criterion, respectively. 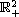Then, we establish sufficient conditions for the global stability of the positive equilibrium by proving the non-existence of closed orbits in the first quadrant $\mathbb{R}^2_{+}$. 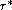Afterwards, we analyze the Hopf bifurcation geometrically by exploring the monotonic property of the trace of the Jacobean matrix with respect to $r$ and analytically verifying that there is a unique $r^*$ such that the trace is equal to 0. We also introduce an auxiliary map by restricting all the five parameters to a special one-dimensional geometrical structure and analyze the Hopf bifurcation with respect to all these five parameters. Finally, some numerical simulations are illustrated which are in agreement with our analytical results.

Submitted March 6, 2016. Published September 21, 2016.
Math Subject Classifications: 34D20, 34E05, 37G15.
Key Words: Density-dependent; local and global stability; Hopf bifurcation; monotonicity; geometrical restriction.

Show me the PDF file (1454 KB), TEX file for this article.

Xin Jiang
School of Mathematics and Systems Science
Beihang University
Beijing 100191, China
email: jiangxin1991@126.com
Zhikun She
School of Mathematics and Systems Science
Beihang University
Beijing 100191, China
email: zhikun.she@buaa.edu.cn
Zhaosheng Feng
School of Mathematical and Statistical Sciences
University of Texas-Rio Grande Valley
Edinburg, TX 78539, USA
email: zhaosheng.feng@utrgv.edu

Return to the EJDE web page