Helge Kristian Jenssen, Charis Tsikkou
Abstract:
Consider the Cauchy problem for the 3-D linear wave equation
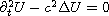 with radial initial data
with radial initial data
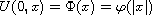 ,
,
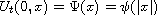 . A standard result states that U belongs
to
. A standard result states that U belongs
to
![$C([0,T];H^s(\mathbb{R}^3))$](gifs/ad.gif) whenever
whenever
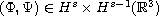 .
In this article we are interested in the question of how U can be realized
as a limit of solutions to initial-boundary value problems on the
exterior of vanishing balls
.
In this article we are interested in the question of how U can be realized
as a limit of solutions to initial-boundary value problems on the
exterior of vanishing balls
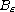 about the origin. We note that,
as the solutions we compare are defined on different domains, the answer
is not an immediate consequence of
about the origin. We note that,
as the solutions we compare are defined on different domains, the answer
is not an immediate consequence of
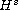 well-posedness for the wave equation.
We show how explicit solution formulae yield convergence and optimal
regularity for the Cauchy solution via exterior solutions, when the latter are
extended continuously as constants on
well-posedness for the wave equation.
We show how explicit solution formulae yield convergence and optimal
regularity for the Cauchy solution via exterior solutions, when the latter are
extended continuously as constants on
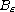 at each time.
We establish that for s=2 the solution U can be realized
as an
at each time.
We establish that for s=2 the solution U can be realized
as an
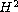 -limit
(uniformly in time) of exterior solutions on
-limit
(uniformly in time) of exterior solutions on
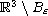 satisfying vanishing Neumann conditions
along
satisfying vanishing Neumann conditions
along
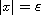 ,
as
,
as
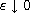 .
Similarly for s=1:
U is then an
.
Similarly for s=1:
U is then an
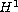 -limit
of exterior solutions satisfying vanishing Dirichlet
conditions along
-limit
of exterior solutions satisfying vanishing Dirichlet
conditions along
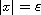 .
.
Submitted July 22, 2016. Published September 30, 2016.
Math Subject Classifications: 35L05, 35L15, 35L20.
Key Words: Linear wave equation; Cauchy problem; radial solutions;
exterior solutions; Neumann and Dirichlet conditions.
Show me the PDF file (283 KB), TEX file for this article.
 |
Helge Kristian Jenssen Department of Mathematics Penn State University, University Park State College, PA 16802, USA email: jenssen@math.psu.edu |
|---|---|
 |
Charis Tsikkou Department of Mathematics West Virginia University Morgantown, WV 26506, USA email: tsikkou@math.wvu.edu |
Return to the EJDE web page