Ming Cheng, Alexander Pankov
Abstract:
This article concerns the periodic discrete Schrödinger equation with
nonlinear hopping on the infinite integer lattice. We obtain the
existence of gap solitons by the linking theorem and concentration compactness
method together with a periodic approximation technique.
In addition, the behavior of such solutions is studied as
.
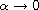Notice that the nonlinear hopping can be sign changing.
Submitted October 7, 2016. Published October 26, 2016.
Math Subject Classifications: 35Q55, 35Q51, 39A12, 39A70, 78A40.
Key Words: Discrete nonlinear Schrödinger equation; nonlinear hopping;
gap soliton; linking theorem; periodic approximation.
Show me the PDF file (242 KB), TEX file for this article.
 |
Ming Cheng College of Mathematics Jilin University Changchun 130012, China email: jlumcheng@hotmail.com |
|---|---|
 |
Alexander Pankov Department of Mathematics Morgan State University Baltimore, MD 21251, USA email: alexander.pankov@morgan.edu |
Return to the EJDE web page