Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 41, pp. 1-12.
Inverse problems associated with the Hill operator
Alp Arslan Kirac
Abstract:
Let
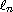 be the length of the
be the length of the
 -th
instability interval of the Hill
operator
-th
instability interval of the Hill
operator
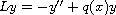 .
We prove that if
.
We prove that if
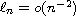 and the set
and the set
 is a subset of the periodic
spectrum of the Hill operator, then
is a subset of the periodic
spectrum of the Hill operator, then
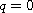 a.e., where
a.e., where
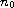 is a sufficiently
large positive integer such that
is a sufficiently
large positive integer such that
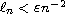 for all
for all
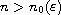 with some
with some
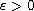 .
A similar result holds for the anti-periodic case.
.
A similar result holds for the anti-periodic case.
Submitted April 29, 2015. Published January 27, 2016.
Math Subject Classifications: 34A55, 34B30, 34L05, 47E05, 34B09.
Key Words: Hill operator; inverse spectral theory; eigenvalue asymptotics;
Fourier coefficients.
Show me the PDF file (245 KB),
TEX file for this article.
 |
Alp Arslan Kiraç
Department of Mathematics
Faculty of Arts and Sciences
Pamukkale University
20070, Denizli, Turkey
email: aakirac@pau.edu.tr
|
|---|
Return to the EJDE web page
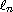 be the length of the
be the length of the
 -th
instability interval of the Hill
operator
-th
instability interval of the Hill
operator
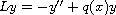 .
We prove that if
.
We prove that if
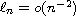 and the set
and the set
 is a subset of the periodic
spectrum of the Hill operator, then
is a subset of the periodic
spectrum of the Hill operator, then
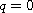 a.e., where
a.e., where
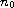 is a sufficiently
large positive integer such that
is a sufficiently
large positive integer such that
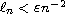 for all
for all
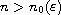 with some
with some
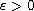 .
A similar result holds for the anti-periodic case.
.
A similar result holds for the anti-periodic case.
