LMPA Laboratory, Department of Mathematics
Jijel University, Algeria
email: norafetou2005@yahoo.fr

LMPA Laboratory, Department of Mathematics
Jijel University, Algeria
email: mfyarou@yahoo.com
Nora Fetouci, Mustapha Fateh Yarou
Abstract: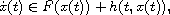
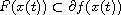 on [0,T], where f is a
primal lower nice function, and h a single valued Caratheodory perturbation.
on [0,T], where f is a
primal lower nice function, and h a single valued Caratheodory perturbation.
Submitted June 15, 2015. Published February 10, 2016.
Math Subject Classifications: 34A60, 49J52.
Key Words: Evolution problem; differential inclusion;
primal lower nice functions; Caratheodory perturbation.
Show me the PDF file (207 KB), TEX file, and other files for this article.
| Nora Fetouci LMPA Laboratory, Department of Mathematics Jijel University, Algeria email: norafetou2005@yahoo.fr | |
 |
Mustapha Fateh Yarou LMPA Laboratory, Department of Mathematics Jijel University, Algeria email: mfyarou@yahoo.com |
Return to the EJDE web page