In this article, we study the existence of nontrivial solutions for the problem
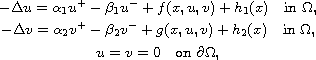
where
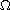 is a bounded domain in
is a bounded domain in
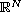 ,
and
,
and
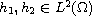 .
Here
.
Here
![$[ \alpha_j,\beta _j] \cap \sigma(-\Delta)={\lambda}$](gifs/ae.gif) ,
where
,
where
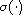 is the spectrum.
We use the Leray-Schauder degree theory.
is the spectrum.
We use the Leray-Schauder degree theory.
Hakim Lakhal, Brahim Khodja
Abstract:
In this article, we study the existence of nontrivial solutions for the problem
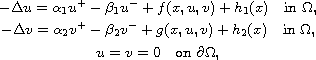
where
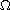 is a bounded domain in
is a bounded domain in
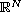 ,
and
,
and
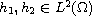 .
Here
.
Here
![$[ \alpha_j,\beta _j] \cap \sigma(-\Delta)={\lambda}$](gifs/ae.gif) ,
where
,
where
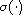 is the spectrum.
We use the Leray-Schauder degree theory.
is the spectrum.
We use the Leray-Schauder degree theory.
Submitted July 26, 2015. Published March 15, 2016.
Math Subject Classifications: 35Q30, 65N12, 65N30, 76M25.
Key Words: Topological degree; elliptic systems; homotopy.
Show me the PDF file (232 KB), TEX file for this article.
 |
Hakim Lakhal Université de Skikda B.P. 26 route d'El-Hadaiek, 21000, Algérie email: H.lakhal@univ-skikda.dz |
|---|---|
 |
Brahim Khodja Badji Mokhtar University P.O. 12 Annaba, Algeria email: brahim.khodja@univ-annaba.org |
Return to the EJDE web page