We use a new variational principle to obtain a positive solution of
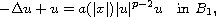
with Neumann boundary conditions where
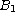 is the unit ball in
is the unit ball in
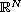 ,
a is nonnegative, radial and increasing and
,
a is nonnegative, radial and increasing and
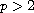 .
Note that for
.
Note that for
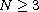 this includes supercritical values of p.
We find critical points of the functional
this includes supercritical values of p.
We find critical points of the functional
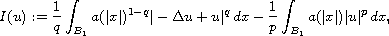
over the set of
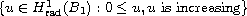 ,
where q is the conjugate of p. We would like to emphasize the energy
functional I is different from the standard Euler-Lagrange functional
associated with the above equation, i.e.
,
where q is the conjugate of p. We would like to emphasize the energy
functional I is different from the standard Euler-Lagrange functional
associated with the above equation, i.e.
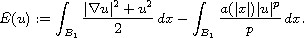
The novelty of using I instead of E is the hidden symmetry in I generated by
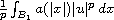 and its Fenchel dual.
Additionally we are able to prove the existence of a positive nonconstant
solution,
in the case a(|x|)=1, relatively easy and without needing to cut off the
supercritical nonlinearity.
Finally, we use this new approach to prove existence results for
gradient systems with supercritical nonlinearities.
and its Fenchel dual.
Additionally we are able to prove the existence of a positive nonconstant
solution,
in the case a(|x|)=1, relatively easy and without needing to cut off the
supercritical nonlinearity.
Finally, we use this new approach to prove existence results for
gradient systems with supercritical nonlinearities.