Fengjuan Meng, Fubao Zhang, Yuanyuan Zhang
Abstract:
In this article, we study the multiplicity of positive solutions for the
biharmonic equation of Kirchhoff type involving concave-convex nonlinearities,
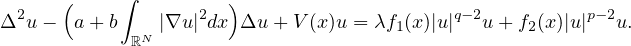
Using the Nehari manifold, Ekeland variational principle, and the theory
of Lagrange multipliers, we prove that there are at least two positive solutions,
one of which is a positive ground state solution.
Submitted March 11, 2019. Published May 19, 2020.
Math Subject Classifications: 35J35, 35J40, 35J91.
Key Words: Biharmonic equation; ground state solution; Nehari manifold;
concave-convex nonlinearity.
DOI: 10.58997/ejde.2020.44
Show me the PDF file (370 KB), TEX file for this article.
 |
Fengjuan Meng School of Mathematics and Physics Jiangsu University of Technology Changzhou 213001, China email: fjmeng@jsut.edu.cn |
|---|---|
 |
Fubao Zhang School of Mathematics Southeast University Nanjing 210096, China email: 101009933@seu.edu.cn |
 |
Yuanyuan Zhang School of Business Jiangsu University of Technology Changzhou 213001, China email: zyylhh1227@163.com |
Return to the EJDE web page