Electron. J. Differential Equations,
Vol. 2020 (2020), No. 46, pp. 1-18.
Global stability of traveling waves for delay reaction-diffusion systems
without quasi-monotonicity
Si Su, Guo-Bao Zhang
Abstract:
This article concerns the global stability of traveling waves of a reaction-diffusion
system with delay and without quasi-monotonicity. We prove that the traveling
waves (monotone or non-monotone) are exponentially stable in
 with the exponential convergence rate
with the exponential convergence rate
 for some constant
for some constant
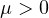 .
We use the Fourier transform and the weighted energy method with a suitably weight
function.
.
We use the Fourier transform and the weighted energy method with a suitably weight
function.
Submitted December 8, 2019. Published May 19, 2020.
Math Subject Classifications: 35C07, 35B35, 92D30.
Key Words: Delay reaction-diffusion system; traveling waves; global stability;
Fourier transform; weighted energy method.
DOI: 10.58997/ejde.2020.46
Show me the PDF file (382 KB),
TEX file for this article.
 |
Si Su
College of Mathematics and Statistics
Northwest Normal University
Lanzhou, Gansu 730070, China
email: 18809422634@163.com
|
|---|
 |
Guo-Bao Zhang
College of Mathematics and Statistics
Northwest Normal University
Lanzhou, Gansu 730070, China
email: zhanggb2011@nwnu.edu.cn
|
|---|
Return to the EJDE web page
 with the exponential convergence rate
with the exponential convergence rate
 for some constant
for some constant
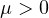 .
We use the Fourier transform and the weighted energy method with a suitably weight
function.
.
We use the Fourier transform and the weighted energy method with a suitably weight
function.

