Electron. J. Differential Equations, Vol. 2020 (2020), No. 52, pp. 1-21.
Existence of weak solutions to superlinear elliptic systems without
the Ambrosetti-Rabinowitz condition
Xiaohui Wang, Peihao Zhao
Abstract:
In this article, we study the existence of the weak solution for
superlinear elliptic equations and systems without the Ambrosetti-Rabinowitz condition.
The Ambrosetti-Rabinowitz condition guarantees the boundedness of the PS sequence
of the functional I for the corresponding problem.
We establish the existence of the weak solution for the superlinear elliptic equation
by using
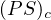 form of the Mountain pass lemma, and the existence of the
weak solution for the superlinear elliptic system by using
form of the Mountain pass lemma, and the existence of the
weak solution for the superlinear elliptic system by using
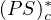 form
of the Linking theorem.
form
of the Linking theorem.
Submitted May 8, 2018. Published May 27, 2020.
Math Subject Classifications: 35J20, 35J47, 35J15, 35A15.
Key Words: Superlinear elliptic system; weak solution;
mountain pass lemma; linking theorem.
DOI: 10.58997/ejde.2020.52
Show me the PDF file (379 KB),
TEX file for this article.
 |
Xiaohui Wang
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: xiaohuiwang1@126.com
|
|---|
 |
Peihao zhao
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: zhaoph@lzu.edu.cn
|
|---|
Return to the EJDE web page
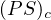 form of the Mountain pass lemma, and the existence of the
weak solution for the superlinear elliptic system by using
form of the Mountain pass lemma, and the existence of the
weak solution for the superlinear elliptic system by using
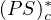 form
of the Linking theorem.
form
of the Linking theorem.

