Let u be a solution to the initial-value problem
![$$u''(t) + {N-1 \over t}u'(t) + u(t) + u(t)|u(t)|^{4/(N-2)} = 0,
\quad t \in (0,T] $$](gifs/ab.gif)
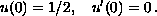
In this paper we show that if
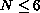 , then the
distance between the two
consecutive zeroes of u is "close" to
, then the
distance between the two
consecutive zeroes of u is "close" to
 .
The proof is based
on an energy analysis and the Sturm comparison theorem.
.
The proof is based
on an energy analysis and the Sturm comparison theorem.
Alexandra Kurepa & Hugh Weithers
Abstract:
Let u be a solution to the initial-value problem
![$$u''(t) + {N-1 \over t}u'(t) + u(t) + u(t)|u(t)|^{4/(N-2)} = 0,
\quad t \in (0,T] $$](gifs/ab.gif)
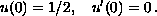
In this paper we show that if
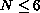 , then the
distance between the two
consecutive zeroes of u is "close" to
, then the
distance between the two
consecutive zeroes of u is "close" to
 .
The proof is based
on an energy analysis and the Sturm comparison theorem.
.
The proof is based
on an energy analysis and the Sturm comparison theorem.
Published November 24, 1999.
Subject lassfications: 34B15, 34A10, 35J65.
Key words: critical exponent, singular equation, Sturm comparison theorem.
Show me the PDF file (123K), TEX file, and other files for this article.
 |
Alexandra Kurepa Department of Mathematics North Carolina A&T State University Greensboro, North Carolina 27411 , USA e-mail: kurepa@ncat.edu |
 |
Hugh Weithers Raytheon AIS, Software Engineer II e-mail: Weithersho@gvl.esys.com hugholu@aol.com Tel: 903-457-6048 |
Return to the EJDE web page