Nonlinear Differential Equations,
Electron. J. Diff. Eqns., Conf. 05, 2000, pp. 1-12.
Explicit construction, uniqueness, and bifurcation curves
of solutions for a nonlinear Dirichlet problem in a ball
Horacio Arango & Jorge Cossio
Abstract:
This paper presents a method for the explicit construction of
radially symmetric solutions to the semilinear elliptic problem

where
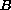 is a ball in
is a ball in
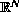 and
and
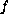 is a continuous
piecewise linear function. Our construction method is inspired
on a result by E. Deumens and H. Warchall [8], and uses spline
of Bessel's functions. We prove uniqueness of solutions for this
problem, with a given number of nodal regions and different sign at
the origin. In addition, we give a bifurcation diagram when
is a continuous
piecewise linear function. Our construction method is inspired
on a result by E. Deumens and H. Warchall [8], and uses spline
of Bessel's functions. We prove uniqueness of solutions for this
problem, with a given number of nodal regions and different sign at
the origin. In addition, we give a bifurcation diagram when
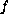 is
multiplied by a parameter.
is
multiplied by a parameter.
Published Ocotber 24, 2000.
Math Subject Classifications: 35B32, 35J60, 65D07, 65N99.
Key Words: Nonlinear Dirichlet problem, radially symmetric solutions,
bifurcation, explicit solutions, spline.
Show me the
PDF file (142K),
TEX file, and other files for this article.
 |
Horacio Arango
Departamento de Matematicas
Universidad Nacional de Colombia
Apartado Aereo 3840
Medellin, Colombia |
 |
Jorge Cossio
Departamento de Matematicas
Universidad Nacional de Colombia
Apartado Aereo 3840
Medellin, Colombia
e-mail: jcossio@perseus.unalmed.edu.co |
Return to the EJDE web page

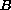 is a ball in
is a ball in
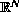 and
and
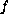 is a continuous
piecewise linear function. Our construction method is inspired
on a result by E. Deumens and H. Warchall [8], and uses spline
of Bessel's functions. We prove uniqueness of solutions for this
problem, with a given number of nodal regions and different sign at
the origin. In addition, we give a bifurcation diagram when
is a continuous
piecewise linear function. Our construction method is inspired
on a result by E. Deumens and H. Warchall [8], and uses spline
of Bessel's functions. We prove uniqueness of solutions for this
problem, with a given number of nodal regions and different sign at
the origin. In addition, we give a bifurcation diagram when
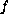 is
multiplied by a parameter.
is
multiplied by a parameter. 
