A real-valued function
 is said to be infinity harmonic if it
solves the nonlinear degenerate elliptic equation
is said to be infinity harmonic if it
solves the nonlinear degenerate elliptic equation 
in the viscosity sense. This is equivalent to the requirement that
 enjoys comparison with cones,
an elementary notion explained below. Perhaps the primary open problem
concerning infinity harmonic functions is to determine whether or not
they are continuously differentiable. Results in this note reduce the
problem of whether or not a function
enjoys comparison with cones,
an elementary notion explained below. Perhaps the primary open problem
concerning infinity harmonic functions is to determine whether or not
they are continuously differentiable. Results in this note reduce the
problem of whether or not a function
 which enjoys comparison with cones has a derivative at a point
which enjoys comparison with cones has a derivative at a point
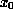 in its domain to determining whether or not maximum points of
in its domain to determining whether or not maximum points of
 relative to spheres centered at
relative to spheres centered at
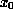 have a limiting direction as the radius shrinks to zero.
have a limiting direction as the radius shrinks to zero.