2001-Luminy conference on Quasilinear Elliptic and Parabolic Equations
and Systems
Electron. J. Diff. Eqns., Conf. 08, 2002, pp. 9-22.
Semi-classical analysis and vanishing properties of
solutions to quasilinear equations
Yves Belaud
Abstract:
Let
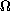 be an open bounded subset of
be an open bounded subset of
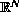 and
and
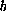 a measurable nonnegative function in
a measurable nonnegative function in
 .
We deal with the time compact support property for
.
We deal with the time compact support property for
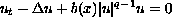
for
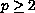 and
and
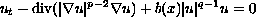
with
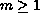 where
where
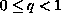 .
We give criteria associated to the first eigenvalue of some
quasilinear Schrodinger operators in semi-classical limits. We
also provide a lower bound for this eigenvalue.
.
We give criteria associated to the first eigenvalue of some
quasilinear Schrodinger operators in semi-classical limits. We
also provide a lower bound for this eigenvalue.
Show me the
PDF file (242K),
TEX file, and other files for this article.
 |
Yves Belaud
Laboratoire de Mathematiques et Physique Theorique
CNRS ESA 6083
Faculte des Sciences et Techniques
Universite Francois Rabelais, 37200 Tours
e-mail: belaud@univ-tours.fr |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
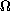 be an open bounded subset of
be an open bounded subset of
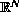 and
and
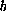 a measurable nonnegative function in
a measurable nonnegative function in
 .
We deal with the time compact support property for
.
We deal with the time compact support property for
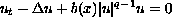
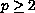 and
and 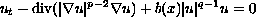
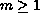 where
where
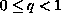 .
We give criteria associated to the first eigenvalue of some
quasilinear Schrodinger operators in semi-classical limits. We
also provide a lower bound for this eigenvalue.
.
We give criteria associated to the first eigenvalue of some
quasilinear Schrodinger operators in semi-classical limits. We
also provide a lower bound for this eigenvalue.
