2001-Luminy conference on Quasilinear Elliptic and Parabolic Equations
and Systems
Electron. J. Diff. Eqns., Conf. 08, 2002, pp. 103-120.
Geometry of the energy functional and the Fredholm alternative for
the p-Laplacian in higher dimensions
Pavel Drabek
Abstract:
In this paper we study Dirichlet
boundary-value problems, for the p-Laplacian, of the form
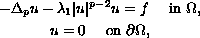
where
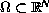 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary
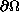 ,
,
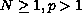 ,
,
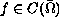 and
and
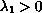 is the first eigenvalue of
is the first eigenvalue of
 . We study the
geometry of the energy functional
. We study the
geometry of the energy functional
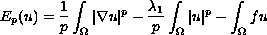
and show the difference between the case
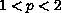 and the case
and the case
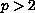 .
We also give the characterization of the right hand sides
.
We also give the characterization of the right hand sides
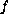 for
which the Dirichlet problem above is solvable and has multiple solutions.
for
which the Dirichlet problem above is solvable and has multiple solutions.
Show me the
PDF file (258K),
TEX file, and other files for this article.
 |
Pavel Drabek
Centre of Applied Mathematics
University of West Bohemia
P. O. Box 314, 306 14 Plzen, Czech Republic
e-mail: pdrabek@kma.zcu.cz
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
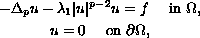
 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary
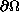 ,
,
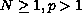 ,
,
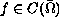 and
and
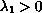 is the first eigenvalue of
is the first eigenvalue of
 . We study the
geometry of the energy functional
. We study the
geometry of the energy functional
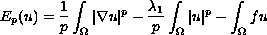
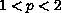 and the case
and the case
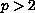 .
We also give the characterization of the right hand sides
.
We also give the characterization of the right hand sides
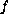 for
which the Dirichlet problem above is solvable and has multiple solutions.
for
which the Dirichlet problem above is solvable and has multiple solutions.
