Problems of existence of the singular spectrum on the continuous spectrum emerges in some mathematical aspects of quantum scattering theory and quantum solid physics. In the latter field, this phenomenon results from physical effects such as the Anderson transitions in dielectrics. In the study of this problem, selfadjoint Friedrichs model operators play an important part and constitute quite an apt model of real quantum Hamiltonians. The Friedrichs model and the Schrodinger operator are related via the integral Fourier transformation. Similarly, the relationship between the Friedrichs model and the one dimensional discrete Schrodinger operator on
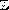is established with the help of the Fourier series.
We consider a family of selfadjoint operators of the Friedrichs model.
These absolute type operators have one singular point
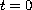of
positive order. We find conditions that guarantee the absence of
point spectrum and the singular continuous spectrum for such operators
near the origin. These conditions are actually necessary and sufficient.
They depend on the finiteness of the rank of a perturbation operator
and on the order of singularity. The sharpness of these conditions
is confirmed by counterexamples.
