In this paper, we give a sufficient conditions for the exact controllability of the non-linear generalized damped wave equation
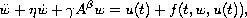
on a Hilbert space. The distributed control
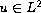 and the
operator
and the
operator
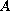 is positive definite self-adjoint unbounded with
compact resolvent. The non-linear term
is positive definite self-adjoint unbounded with
compact resolvent. The non-linear term
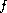 is a continuous
function on
is a continuous
function on
 and globally Lipschitz in the other variables.
We prove that the linear system and the non-linear system are both
exactly controllable; that is to say, the controllability of
the linear system is preserved under the non-linear perturbation
and globally Lipschitz in the other variables.
We prove that the linear system and the non-linear system are both
exactly controllable; that is to say, the controllability of
the linear system is preserved under the non-linear perturbation
 .
As an application of this result one can prove the exact controllability
of the Sine-Gordon equation.
.
As an application of this result one can prove the exact controllability
of the Sine-Gordon equation.
