Sixth Mississippi State Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 15 (2007), pp. 107-126.
Positive solutions for elliptic problems with critical
indefinite nonlinearity in bounded domains
Jacques Giacomoni, Jyotshana V. Prajapat, Mythily Ramaswamy
Abstract:
In this paper, we study the semilinear elliptic problem with critical
nonlinearity and an indefinite weight function, namely
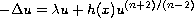
in a smooth open bounded domain
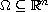 ,
,
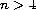 with Dirichlet boundary conditions and for
with Dirichlet boundary conditions and for
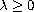 .
Under suitable assumptions on the weight function, we obtain
the positive solution branch, bifurcating from the first
eigenvalue
.
Under suitable assumptions on the weight function, we obtain
the positive solution branch, bifurcating from the first
eigenvalue
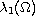 . For
. For
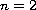 ,
we get similar results for
,
we get similar results for
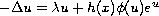 where
where
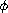 is bounded and superlinear near zero.
is bounded and superlinear near zero.
Published February 28, 2007.
Math Subject Classifications: 35J60, 35B45, 35B33, 35B32.
Key Words: Critical indefinite nonlinearity; bifurcation; a priori estimates.
Show me the
PDF file (357K),
TEX file for this article.
| |
Jacques Giacomoni
MIP-CEREMATH/bat C, Manufacture des Tabacs
Allée de Brienne 21
31000 Toulouse, France
email: giacomo4@yahoo.fr |
|---|
 |
Jyotshana V. Prajapat
School of Mathematics
Tata Institute of Fundamental Research
Homi Bhabha Road, Mumbai 400 005, India
email: jyotsna@math.tifr.res.in |
|---|
 |
Mythily Ramaswamy
TIFR Center, IISc. Campus
Bangalore 560 012, India
email: mythily@math.tifrbng.res.in |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
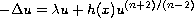
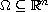 ,
,
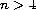 with Dirichlet boundary conditions and for
with Dirichlet boundary conditions and for
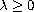 .
Under suitable assumptions on the weight function, we obtain
the positive solution branch, bifurcating from the first
eigenvalue
.
Under suitable assumptions on the weight function, we obtain
the positive solution branch, bifurcating from the first
eigenvalue
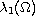 . For
. For
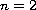 ,
we get similar results for
,
we get similar results for
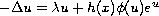 where
where
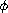 is bounded and superlinear near zero.
is bounded and superlinear near zero.

